The basic idea is that for a specific wavelength, the response of the spectrograph to a certain input illumination can be described by a 3x3 transformation matrix and a subsequent convolution with a point spread function (PSF). Both, the transformation matrices and the PSFs are therefore wavelength dependent. It is reasonable to assume that along a single echelle order, the PSFs and transformation parameters will vary smoothly. If we know the matrices and PSFs for a sufficient large number of wavelength, we can interpolate between them for arbitrary wavelength.

The input of a spectrograph is either a fiber (or multiple fibers) or a slit, but can in either case be represented by a 2D array with a certain illumination. The illumination pattern is always confined within a rectangular bounding box. The mapping of this rectangular array and the spectrograph detector is described by a transformation matrix.

Transformation matrices

At a monochromatic wavelength, the information about the mapping of the input slit / fiber onto the detector of the spectrograph can be described by a 3x3 transformation matrix. In principle there are two geometric transformation we could choose from: Affine and projective transformation. While the latter is more general, we found that affine transformations are sufficiently accurate to describe the spectrograph optics. 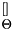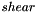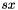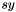Affine transformation parameters also give an intuitive insight in what happens across an order, because they can be expressed in terms of rotation( $\Theta$ ), shear ( $shear$ ), scaling in both directions ( $sx$ and $sy$ ) and translation ( 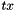$tx$ and $ty$ ) .

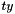There is no unique definition of how do compose an affine transformation matrix, we will use the following:

$M_{\lambda} = \begin{pmatrix} sx \cdot \cos(\Theta) & -sy \cdot \sin(\Theta+shear) & tx \\ sx \cdot \sin(\Theta) & sy \cdot \cos(\Theta+shear) & ty \\ 0 & 0 & 1 \end{pmatrix}$

We choose to calculate the wavelength dependent transformation parameters by tracing the 4 corner points as well as the center of the input field (i.e. fiber/slit) through ZEMAX and obtain the transformation matrices. In principle the matrices could also come from an analytical description, as long as it delivers a 3x3 matrix for a given order and wavelength.

Using the ZEMAX model makes sure that the best optical description available is used to generate the matrices.

As an example, we plot the scale parameter in x-direction (dispersion direction) as a function of wavelength for the MaroonX spectrograph. Data of the same echelle order are connected by a line. The anamorphic magnification of the spectrograph is directly reflected by an increase of sx across each order. On the right plot we see sx for order 100. Note that the increase of sx with wavelength is not a linear, but a smooth function.

Bokeh Plot

Point Spread Function

While the transformation matrix describes well the coarse behaviour of a spectrograph at a specific wavelength, we need additional information to account for all optical aberrations that occur in a realistic spectrograph. The point spread function (or PSF) is defined as the response of an optical system to a point source.

Casually speaking, the PSF leads to a blur of the imaged input slit. In a spectrograph, this blur of the PSF will usually be of the same size or smaller than the size of the input slit on the detector.

The shape of the PSF can have a complex form, and using a simple Gaussian function might not accurately describe the PSF. The PSF will vary in form and size across the detector, depending on the subtleties of the optics for a specific wavelength.

This makes it difficult to describe the PSF in a general analytic form. Therefore, we use a numeric 2D array on an oversampled grid (compared to the detector's natural grid) to describe the PSFs.

In order to interpolate between two PSFs, we calculate the normalized linear sum of the two neighbouring PSFs. (see also PSF_ZEMAX::interpolate_PSF)